blogブログ
僕が好きな放物線の小ネタ3選<#日曜数学 #アドベントカレンダー>
2017年12月15日
※本記事は横山明日希が過去運営しておりましたブログからの再掲記事になります。(2017.12)
この記事は、日曜数学 Advent Calendar 2017 の5日目の記事です。 昨日は@kiguro_masanaoさんの「ピタゴラスの定理のとある拡張」でした。
はじめましての方ははじめまして。 n度目の方はこんにちは。 数学の楽しさを伝える数学のお兄さんです。 久々にブログ記事を書きます。 突然ですが、あなたは放物線、感じてますか? 一番みんなが放物線を感じる時は、こういう時でしょうか。

「わたしの投げるボールの方が描く放物線の方が2次の変数における係数が小さ〜い!」 「このやろー!俺ももっと係数小さくできるわー!」 「「きゃっきゃっ♪」」 …まあこんな経験している人はいないと思いますが、モノを投げた時のそのモノが動く軌跡が放物線になりますね。 そんな放物線を普段感じている方もそうでない方も、 この記事で放物線のことが今よりも好きになれるはずです。 僕が好きな放物線の小ネタ3つをご紹介します!
1.放物線の一般式、それぞれの係数を動かすと…?
まずは一つ目。こちらの式に注目します。 ![]() そう、放物線(二次関数)の一般式。この係数(aやbやc)は色々な値を取りうるのですが、この値を変えていくことで放物線の形が変わります。 たとえばcを動かすとグラフはこのように動きます。
そう、放物線(二次関数)の一般式。この係数(aやbやc)は色々な値を取りうるのですが、この値を変えていくことで放物線の形が変わります。 たとえばcを動かすとグラフはこのように動きます。
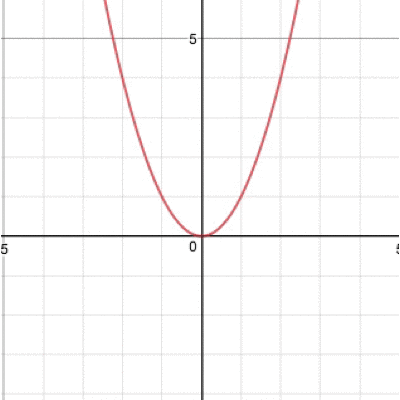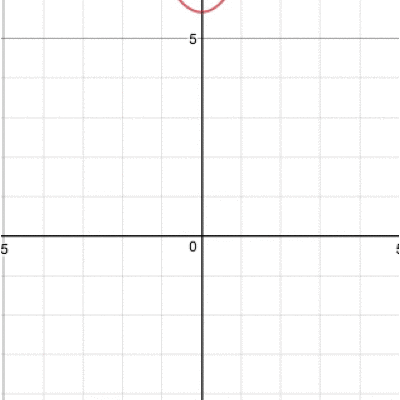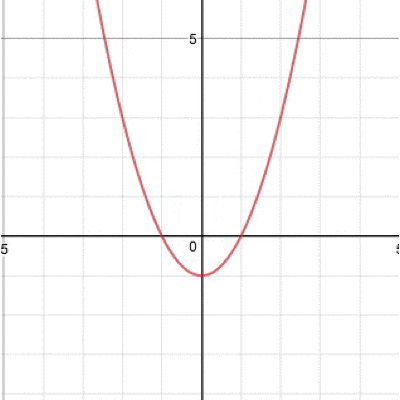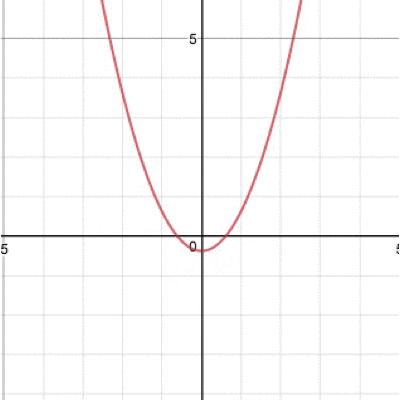
そう、グラフが上下に動きますね。続いてaを動かすと、
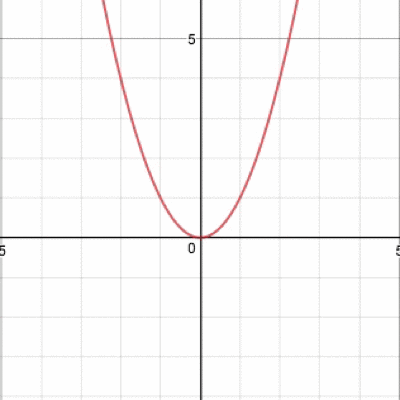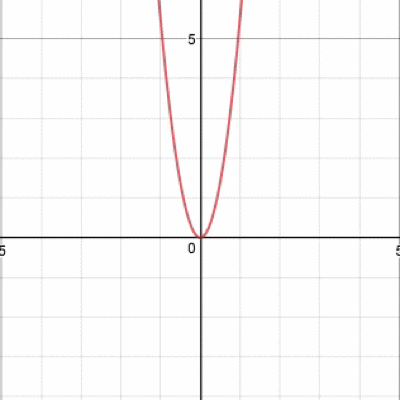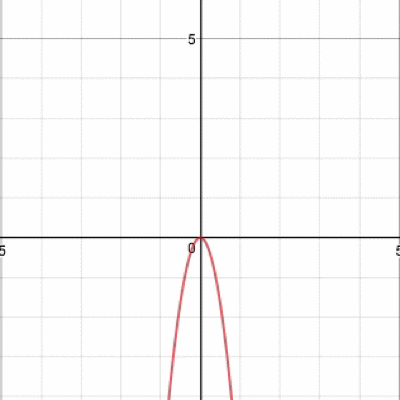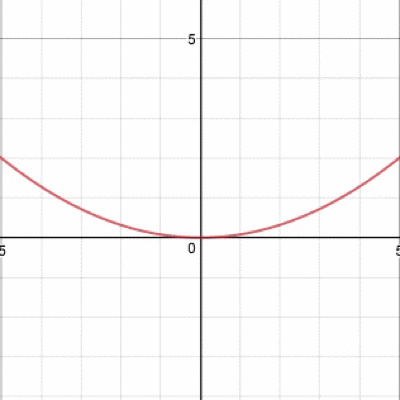
グラフが開いたり閉じたりひっくり返ったり…そんな動きをするわけですね。 では、最後、bを動かすとどうなるでしょうか。 実際に動かしたグラフがこちら。
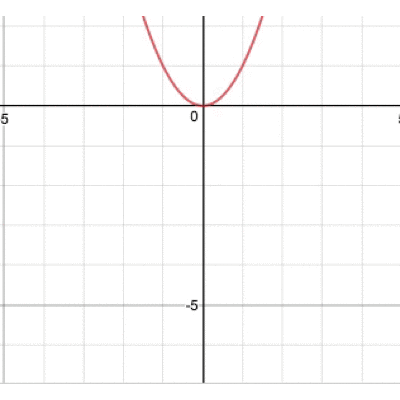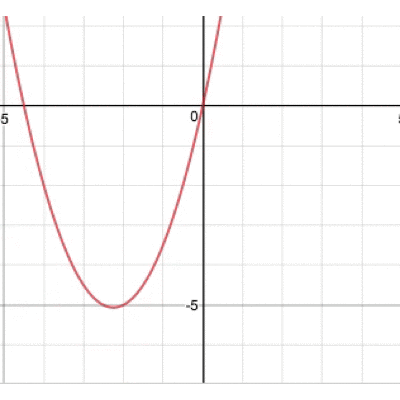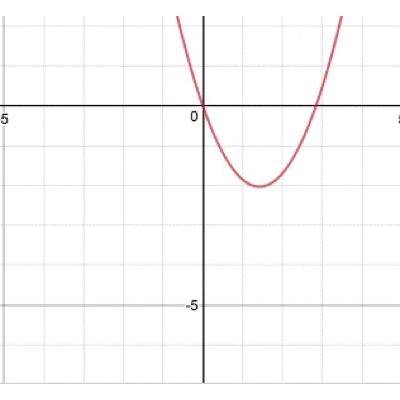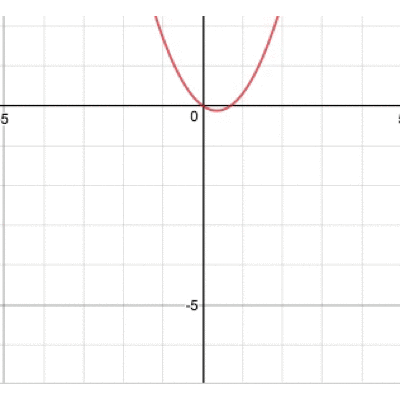
この動き、ちょっと不思議ですよね。どんな動きをしているのでしょうか。 実は、この放物線の頂点に注目すると動きが見えてきます。 その図がこちら。
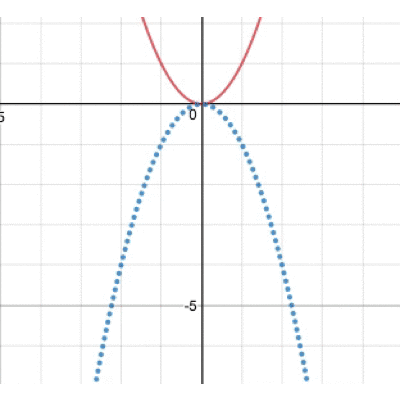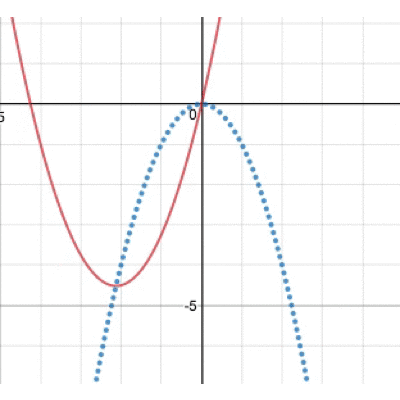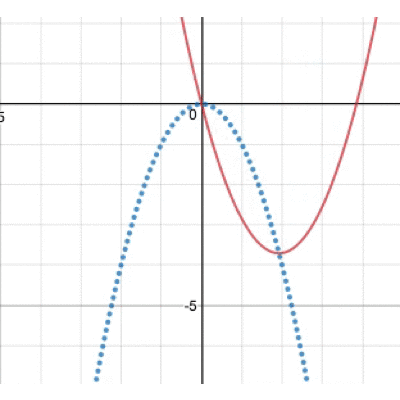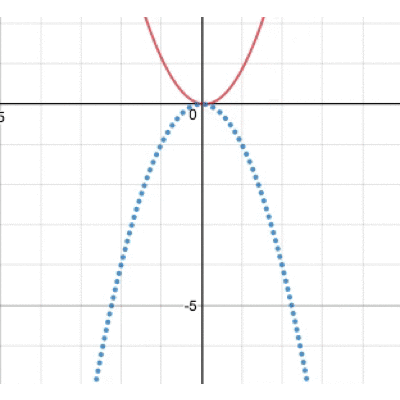
そう、bを動かすと放物線上を放物線が動くことになるんですね!そう思って改めて先ほどの図を眺めてみましょう。しばらく眺めていたくなるはず…笑

2.放物線2つの接線の傾きを簡単に見つける方法?
さて、続いて二つ目。 放物線を2つ並べてみましょう。
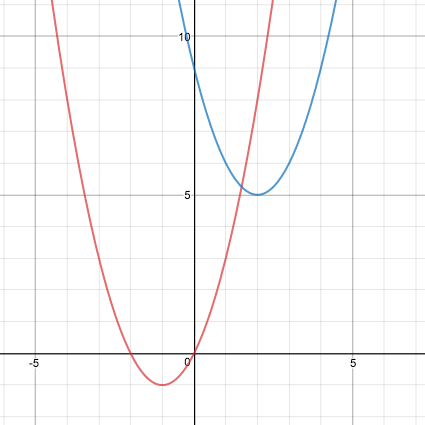
この2つの放物線の接線の傾きはいくつでしょうか? 接戦を引くとこのようになりますね。
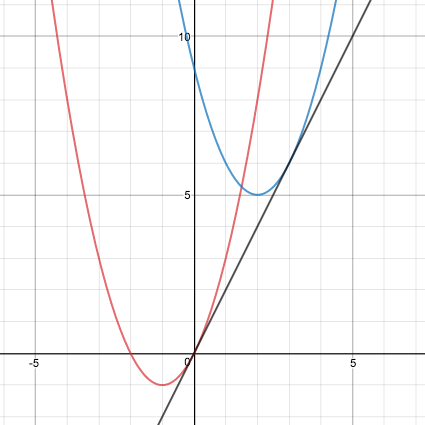
細かい解き方は他のサイトでも探せば出てきますので解き方の方針のみ記載しておくと ①接線をy=mx+nとおく ②この接線の式と放物線それぞれの式で連立する ③判別式=0を考えて、m(傾き)を求める です。 計算に少し時間がかかりそうですね。 でも、実はこのように頂点に注目して頂点どうしを線で結ぶと、
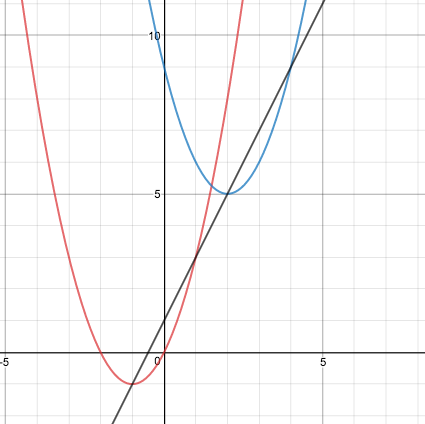
なんとこの頂点を結んだ直線の傾きが、放物線同士の接線の傾きになるという性質があるのです! 図で表すとこんな感じですね。
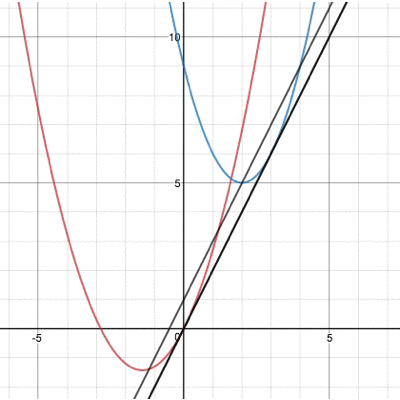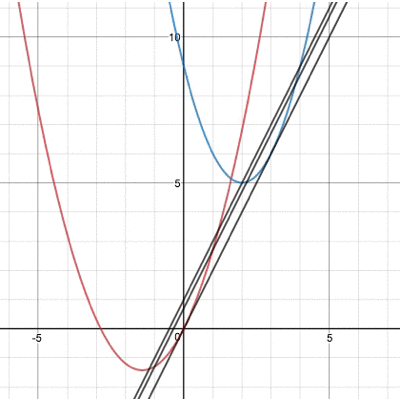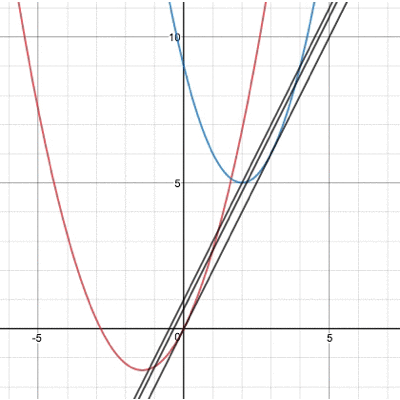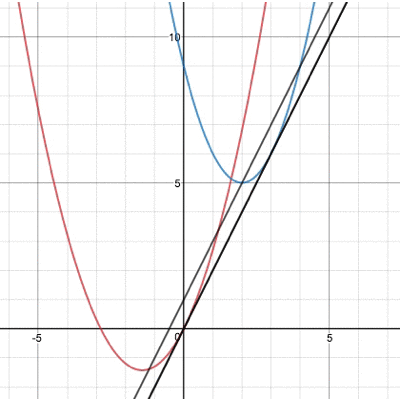
確かに同じ傾きの直線になっていますね。この性質を利用すると ①頂点の座標を平方完成する ②頂点を結ぶ直線の式を作る という流れだけで接線の傾きを求めることができるのです。 接線の式を求めるところまで計算しろ、と言われると同じくらい計算量を必要としますが、傾きを求めるだけだったらこちらの方が圧倒的に早いのです!
3.全ての放物線は相似?
最後に三つ目です。 見出しの通り、全ての放物線が相似なのかどうかという話をします。 まずはこちらの図を見てみましょう。
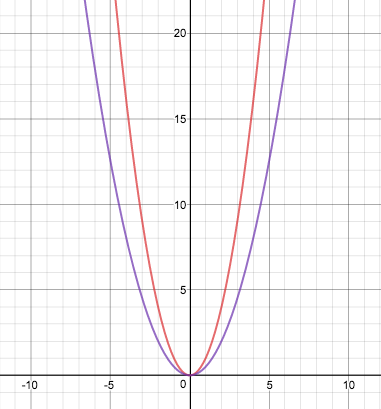
この2つの放物線、直感的には違う図形に見えますね。 ですが、この放物線同士、もっというとあらゆる全ての放物線は相似という性質があるのです! 実際に計算して証明する場合は放物線上に点をとり、放物線と点に注目して拡大し別の放物線に重なるかを確かめる、といった方法があります。もしこの計算して証明する方法を知りたいという人がいたら検索するなりして探してみてください! しかし、この証明だと直感的に放物線が相似であることを理解することが難しいので、ちょっと変わった方法でなんとなく相似であることを理解してもらおうと思います。 その方法がこちら。2つのグラフを見比べてみてください。
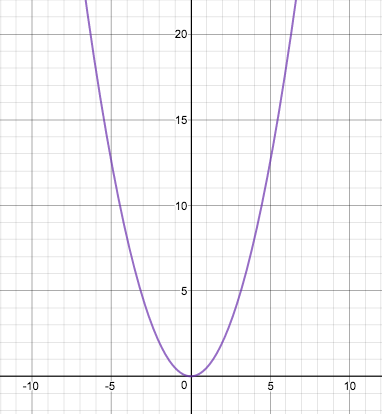
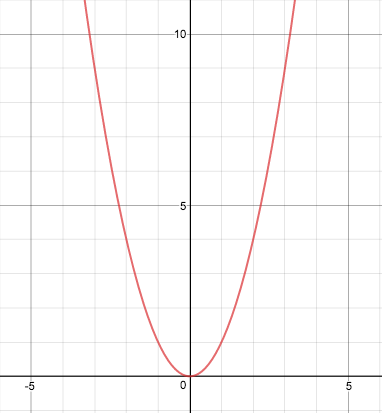
この2つのグラフ、それぞれ違う放物線を表していますね。 ですが、同じ形に見えませんか? 実際に重ね合わせてみると
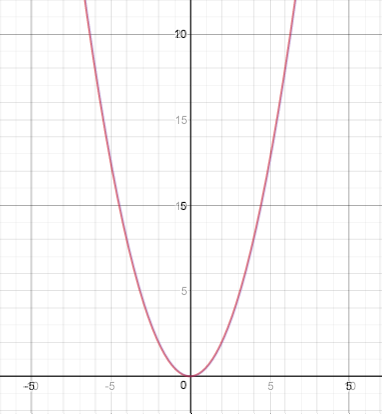
と、ぴったり重なります。(重なりすぎてて見えにくかもですが、座標を見れば課なさっているのがわかるはず)
それもそのはず。この2つの図は同じ形のグラフをもとに、座標の目盛りの幅を変えた図です。そしてこのようにぴったり重なるということは、この2つのグラフは相似といえるのです。
なんで?という方にはもう少しだけ説明を。 2つの図形があり、片方の図形を拡大縮小させることでもう片方の図形と重なる→2つの図形は相似である という論理が通常の相似の考え方です。今回はこの相似の基本的な発想を利用しています。
ちなみにこれをさらに応用させていくと ある1つの図形をもとに、座標の細かさを変える(縦横の細かさは変えない)ことで(図上で)様々な大きさの図形を作る→作った図形は全て相似となる という論理で全ての放物線は相似であることが、なんとなく認識できるはずです!
まとめ
…はい、というわけで「僕が好きな放物線の小ネタ3選」は以上となります。
放物線には色々な面白い性質が潜んでいることが少しだけでも伝わったでしょうか。
今までより少しだけでも放物線のことが好きになれていたのなら幸いです。
以上です!またお会いしましょう!
明日はdafuyafuさんの記事です!
===== この記事は日曜数学 Advent Calendar 2017という企画に参画しており、書かせて頂いております。
日曜数学 Advent Calendar 2017
日曜数学とはなんですか?と思う方もいると思いますが、この日曜数学という言葉を作られた日曜数学会というイベントを主催されるtsujimotterさんは「興味の赴くままに趣味として数学を探求すること」と言っております。
おもに休日に時間をとることが多いことから“日曜”数学と呼ばれ、それらを行う人を「日曜数学者」と、そしてtsujimotterさんが主催されるイベントは「日曜数学会」と名称がついております。 イベントも定期的に行われているのでぜひご覧になってみてください!
=====
最後に一つ宣伝をして終わりたいと思います。 こんな感じの直感的に理解できて笑えたりためになったりする本が、来年1月に発売されることになりました。 僕が所属する日本お笑い数学協会の本『笑う数学』です! ぜひ、ご予約くださいませ〜〜!

